"""2024-01-08
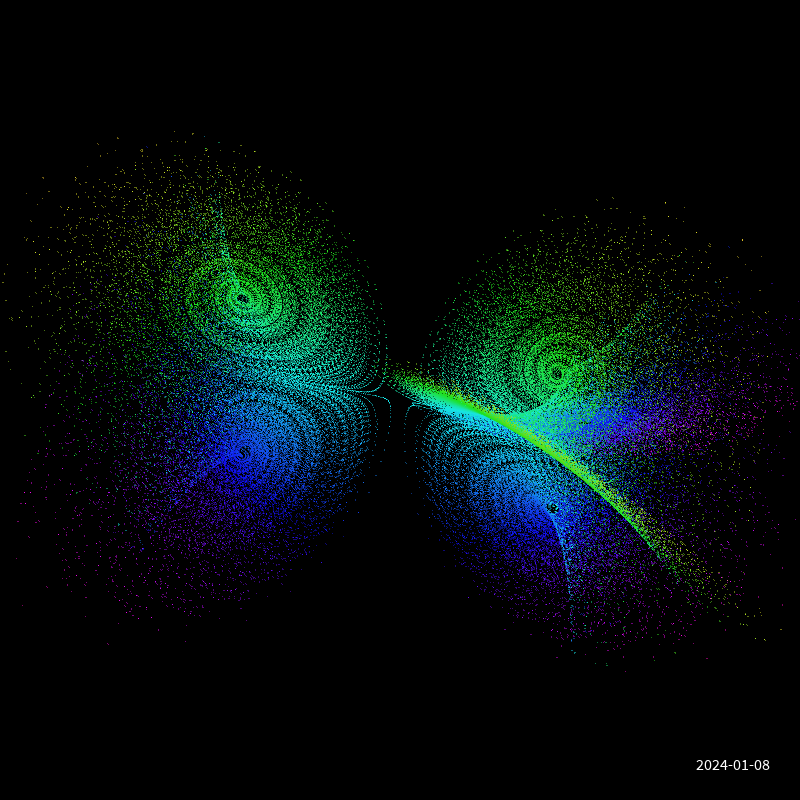
Genuary 08 - Chaotic system
Três atratores de Lorenz, vistos em diferentes perspectivas
png
Sketch,py5,CreativeCoding
"""
import numpy as np
import py5

from utils import helpers

sketch = helpers.info_for_sketch(__file__, __doc__)


def lorenz(xyz, *, s=10, r=28, b=2.667):
    """
    Parameters
    ----------
    xyz : array-like, shape (3,)
       Point of interest in three-dimensional space.
    s, r, b : float
       Parameters defining the Lorenz attractor.

    Returns
    -------
    xyz_dot : array, shape (3,)
       Values of the Lorenz attractor's partial derivatives at *xyz*.
    """
    x, y, z = xyz
    x_dot = s * (y - x)
    y_dot = r * x - y - x * z
    z_dot = x * y - b * z
    return np.array([x_dot, y_dot, z_dot])


def setup():
    py5.size(helpers.LARGURA, helpers.ALTURA, py5.P3D)
    py5.background(0)
    py5.color_mode(py5.HSB, 360, 100, 100)
    dt = 0.02
    num_steps = 40000
    xyzs = np.empty((num_steps + 1, 3))
    xyzs[0] = (1.0, 3.0, 4.05)
    for i in range(num_steps):
        xyzs[i + 1] = xyzs[i] + lorenz(xyzs[i]) * dt
    for rx, ry, rz in (
        (15, -55, 35),
        (-15, 55, -35),
        (-25, 55, 35),
    ):
        with py5.push_matrix():
            py5.translate(py5.width // 2, py5.height // 2, 580)
            py5.rotate_x(py5.radians(rx))
            py5.rotate_y(py5.radians(ry))
            py5.rotate_z(py5.radians(rz))
            for x, y, z in xyzs:
                h = py5.remap(x, -30, 30, 0, 359)
                s = py5.remap(x, -30, 30, 80, 100)
                b = py5.remap(x, -50, 50, 80, 100)
                py5.stroke(h, s, b)
                py5.point(x, y, z)
    helpers.write_legend(sketch=sketch)


def key_pressed():
    key = py5.key
    if key == " ":
        save_and_close()


def save_and_close():
    py5.no_loop()
    helpers.save_sketch_image(sketch)
    py5.exit_sketch()


if __name__ == "__main__":
    py5.run_sketch()